Matematické modelování evoluce agresivity a kooperace
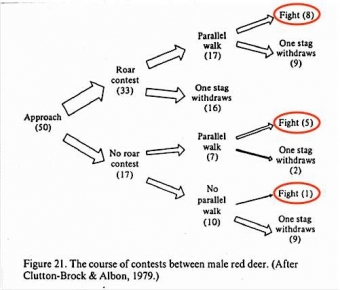
Matematické modely jsou nedílnou součástí evoluční ekologie (Křivan, 2017). U zrodu evoluční teorie her byl následující paradox týkající se řešení konfliktních situací mezi zvířaty. Pro ilustraci uvažujme jeleny, kteří v době říje svádějí souboje o samice. Na základě postulátu o přežívání nejschopnějších by se zdálo, že agresivní chování bude mezi jeleny převažovat. Agresivní samec zraní či zabije svého soka a získá tak jeho samice, čímž zvýší svoji fitness měřenou počtem potomků. Nicméně pozorování ukázala, že tomu tak není a v řadě konfliktů k souboji nedojde, protože zvířata řeší spory vícestupňově. V případě jeleních soubojů o samice dochází k postupné eskalaci konfliktu (např. troubení, paralelní chůze) mezi samci, přičemž jeden ze samců v mnoha případech uteče dříve, než dojde k boji. Někteří etologové toto chování vysvětlovali tak, že z hlediska populace není agresivní strategie dobrá, poněvadž vede ke zranění nebo smrti, a tedy ke snižování velikosti populace (a tedy ke snižování “fitness populace”). Nicméně takové vysvětlení se nezakládá na Darwinově představě, že selekce probíhá na úrovni jedince, tj. cílem je přežití jedince a nikoliv populace. Darwinovské vysvětlení evoluce agresivity bylo vysvětleno pomocí modelu “jestřábi a hrdličky” (“Hawk-Dove game’’). Tento model uvažuje populaci jednoho biologického druhu, ve které se setkávají jedinci dvou různých fenotypů. Zatímco jedinec s fenotypem “hrdlička” pouze předstírá bojovnost, a v případě napadení utíká bez boje, “jestřábi” jsou odhodláni jít do vzájemného souboje. Matematická analýza tohoto modelu ukázala, že (1) v populaci mohou existovat oba dva fenotypy a (2) procentuální zastoupení jedinců typu “jestřáb” se v populaci bude snižovat se zvyšující se pravděpodobností zranění nebo smrti v případě souboje. Z tohoto závěru vycházeli i političtí stratégové během studené války, kteří argumentovali, že čím ničivějšími jadernými zbraněmi budou USA a SSSR disponovat, tím nižší bude pravděpodobnost jejich použití.
Model jestřábi a hrdličky, platí za určitých předpokladů. Mj. předpokládá, že interakce mezi fenotypy trvají stejnou dobu, což ale není nutně pravda. Např. konflikt dvou jedinců typu “jestřáb” může trvat jinou dobu než konflikt dvou jedinců typu “hrdlička”. Zcela nová teorie evolučních her (Křivan a Cressman, 2017), která zahrnuje délku trvání interakcí mezi oponenty ukazuje, že např. dostatečná délka trvání konfliktních situací mezi jedinci typu “jestřáb” vzhledem k ostatním typům interakcí vede k polymorfismu (tj. koexistenci obou fenotypů v populaci) i v těch případech, kdy klasický model predikuje monomorfismus.
Stejná teorie byla aplikována na evoluci kooperace mezi organismy. Klasický model, který se pro vysvětlení evoluce kooperace používá, je tzv. Vězňovo dilema (Prisoner’s dilemma). Vysvětlení evoluce kooperace je obtížné a evoluční biologové hledají mechanismy, které k evoluci kooperace vedou. Práce Křivan a Cressman (2017) přináší nový mechanismus, který je založený na možnosti oponentů ukončit opakující se interakce se stávajícím partnerem a hledáním nového partnera.
Kontakt: Prof. RNDr. Vlastimil Křivan (vlastimil.krivan at prf,jcu.cz)